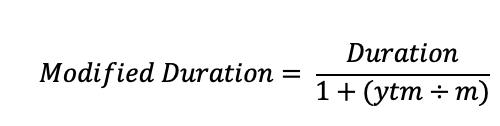The duration of a bond is the weighted average of times each payment happens. Once you know the duration, you can measure how the bond’s price changes when the interest rate changes. Thus, duration measures the riskiness of a bond. The higher the duration, the higher the riskiness.
Maturity, Coupon Rate and Duration
The duration of a bond cannot be larger than the maturity of a bond and cannot be less than 0. It’s always in between. There’s a direct relationship between maturity and duration, but an inverse relationship between coupon rate and duration.
Relationship between maturity and duration: The longer the maturity, the higher the duration
The shorter the maturity, the lower the duration
Relationship between coupon rate and duration: The higher the coupon, the lower the duration because you put less weight on the maturity.
The lower the coupon, the higher the duration, because you put a lot of weight on the maturity.
The above relationship indicates that duration is determined by weights and maturity.
Zero-Coupon Bond
The duration for a zero-coupon bond equals its maturity because there is only one time the payment happens, which is at the maturity of the bond. The bond with the highest duration has to be a zero-coupon bond because the lower the coupon, the higher the duration, and you cannot have a lower coupon than zero.
Example Question:
What is the duration of a four-year $1,000 Treasury bond with a 10 percent semiannual coupon selling at par?
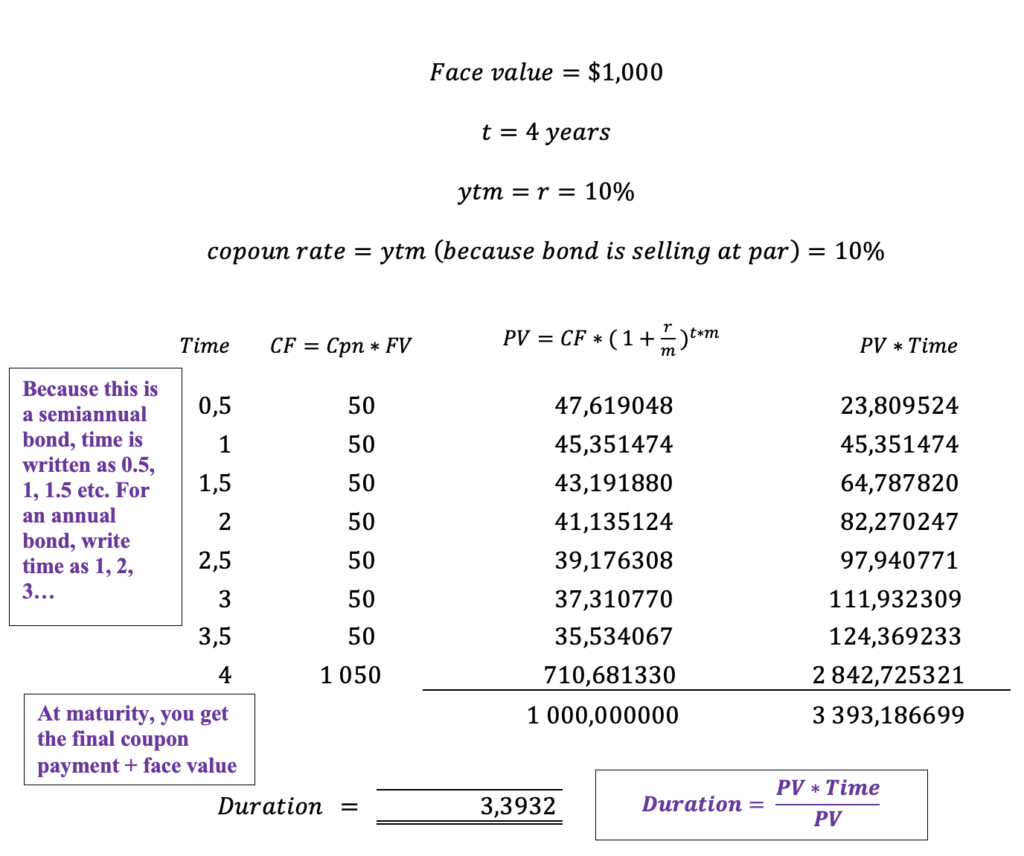
Modified Duration
Modified duration measures the percentage change in the price of a bond for a 1 percentage-point change in yield. For example, id modified duration is 5.47%, this means that a 1% change in the yield to maturity will change the price of the bond by 5.47%.
Formula: